Native
任意一个大于$1$的正整数都能被唯一分解成有限个质数的乘积,可写作:
其中 $c_i$ 都是正整数,$p_i$ 均为质数,且满足 $p_1<p_2<…<p_m$。
推广1:约数个数
先分解质因数,接下来:
推广2:约数和
算法
以下算法用于分解质因数。
试除法-$O(\sqrt{N})$
是一种试除法和埃筛结合的方法,思想如下:
考虑从 $2-\sqrt{N}$ 枚举每个 $d|N$,然后从 $N$ 中除去所有因子 $d$。
复杂度可以保证在稳定的 $O(\sqrt{N})$。
因为一个合数被扫到之前其质因数已经被筛掉了,所以正确性可以保证。
1
2
3
4
5
6
7
8
9
10
| #define MAXN 10050
int p[MAXN],c[MAXN],cnt;
inline void divide(int n){
for(int i=2;i<=sqrt(n);++i)
if(n%i==0){
p[++cnt]=i;
while(n%i==0)n/=i,++c[cnt];
}
if(n>1)p[++m]=n,c[m]=1;
}
|
线筛法
以下的方法都需要使用线筛,如果题目需要筛素数,那顺便用上这些算法是很好的。
如果题目不需要筛素数,但是需要频繁的查询,那么也可以用这些办法预处理求质因数分解。
素数试除线筛-$O(\sqrt N)$ 预处理
可以考虑先把 $\sqrt N$ 范围内的素数给筛出来,然后从第一个素数开始分解直到质数大于 $\sqrt N$ 的时候结束,这样复杂度就是小于 $\sqrt N$ 的素数个数。
记小于 $x$ 的素数个数为 $\omega(x)$,则该算法的复杂度为:
又因为小于$N$的素数约为 $\frac{N}{ln N}$ 个,因此该算法的复杂度大约为 $O(\frac{2\sqrt N}{ln\sqrt N})$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| bitset<MAXN>isPrime;
int Prime[MAXN],cnt;
void GetPrime(int n){
for(int i=2;i<=n;++i){
if(!isPrime[i])Prime[++cnt]=i;
for(int j=1;j<=cnt&&i*Prime[j]<=n;++j) {
isPrime[i*Prime[j]]=1;
if(i%Prime[j]==0)break;
}
}
}
int p[MAXN],c[MAXN],fcnt;
inline void divide(int n){
if(!isPrime[n]){
p[++fcnt]=n;
++c[fcnt];
return;
}
for(int i=Prime[1];Prime[i]<=sqrt(n);++i){
if(n%i==0){
p[++fcnt]=Prime[1];
while(n%i==0)n/=Prime[i],++c[fcnt];
}
}
}
|
质因子线筛-$O(N)$ 预处理
可以考虑在维护线筛的同时,将标记素数的数组变成记录当前数字最小质因数的数组。
这样每次只要让一个数字一直除以自己的最小质因数就可以完成查询,复杂度降低到 $O(log_2N)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| int Prime[MAXN],isPrime[MAXN],cnt;
void GetPrime(int n){
for(int i=2;i<=n;++i){
if(!isPrime[i]){
isPrime[i]=i;
Prime[++cnt]=i;
}
for(int j=1;j<=cnt&&i*Prime[j]<=n;++j) {
isPrime[i*Prime[j]]=Prime[j];
if(i%Prime[j]==0)break;
}
}
}
int c[MAXN];
inline void divide(int n){
GetPrime(n);
for(int i=1;i<=n;++i)
for(int j=i;j!=1;j/=v[j])
++c[v[j]];
}
|
复杂度对比
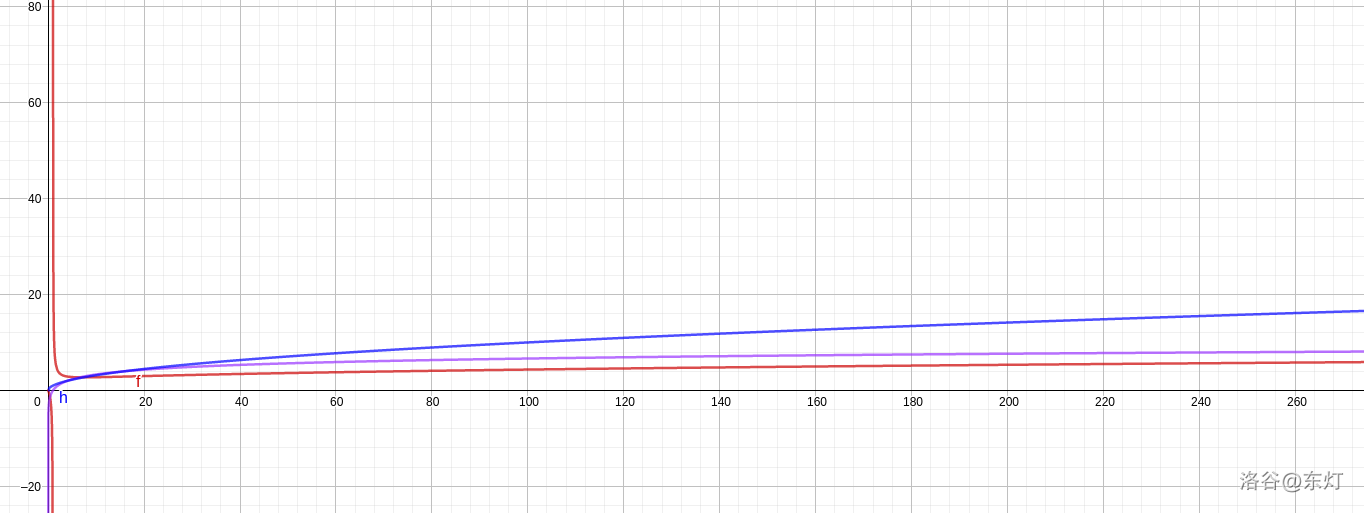
红线为素数试除线筛,紫色为质因子线筛,蓝色为朴素试除法。
Pollard’s Rho-期望$O(N^{\frac{1}{4}})$
待补。
