很久之前就想写一篇这个文章了,但是一直没抽出时间。
今天下午刚好颓废没事做,我们来聊聊这个话题吧。
在切入正题之前我们要先讨论两个问题:
- 何谓 Map?
- 怎么做高效的 Hash?
何谓 Map?
Map 是一类可以映射键值对 $key - value$ 的数据结构,可以使用 $key$ 来查询 $value$ 的值。
理论上能够完成这些事情的数据结构都可以叫做 Map。
而 Map 的速度很大程度上取决于应该如何高效地完成查找 $key$ 所映射的 $value$ 值的过程,HashMap 就是 Map 的一种实现,它的理想复杂度为 $O(1)$。
怎么做高效的 Hash?
Hash 的定义及我们采用的方法
Hash 就是散列,是一个定义很自由的名词,而目的是把一个 $key$ 散列为一个期望范围内的值。
一旦 $key$ 被散列到了一个可以接受的范围内,就代表查找某个 $key$ 时只需要把它重新散列成那个值就可以查找到答案。
可以用鸽笼定理发现的是,一个更大的范围转换到一个更小的范围一定会有很多元素冲突在一个值上,我们将其称为 Hash 碰撞,在出现碰撞时如何解决也是 HashMap 的一个重要工作。
那么对于 HashMap 来说,散列后的范围越大,Hash 散列的方法越优秀,理论上来说发生碰撞的概率就越小,但是相对应的,占用的空间也成本也就越多。
在这里我们介绍一种最常用的散列方法:模数散列法。
其哈希散列函数的定义很简单: $hash(x)=x \ mod \ P$。
其正确性如何证明?考虑一个正整数在经过该函数处理后,一定就散列到了模 $P$ 的剩余系中,散列范围即为 $[0,P-1]$。但是使用这个方法需要注意的是 $P$ 的选取最好是一个大质数,当其为小质数时,可能成为其他大整数的质因子,导致大量值在 $0$ 处堆积;当其不是质数时也会导致碰撞,证明可以见此。
注意到取模运算在 C++ 中的复杂度并不是很优秀,我们需要对这个方法进行一些改造,运用一个性质:当今且仅当 $P=2^n-1$ 时,$x\&P=x \ mod \ 2^n$。
因此我们可以直接选择模数为 $2^n-1$,用按位与解决该问题。这时候读者可能有一个疑问:如何保证 $2^n$ 不是质数不是散列出来的效果不好吗?那…其实你把这个值选的比较大别人就卡不掉了!
而且目前的 $OI$ 界一般没有针对这个模数的碰撞数据,因为如果需要卡碰撞,会卡常规方法写出来的碰撞,出题人很难猜到有人用这种邪门的散列思路,想到了也觉得应该先把常规的方法卡掉再卡这种方法,因此一般来说采用 $2^n$ 作为模数来散列在算法竞赛中是不会被卡的。
效率比较
我们来比较取模和按位与的效率,下面是比较采用的代码:
(为了避免编译器优化已知模数,这里我们采用输入方法读入模数,而且为了避免编译器直接把这个循环优化掉,我们要输出最后的结果)
1 | unsigned long long end=1e8,mod,ans(0); |
1 | unsigned long long end=1e8,mod,ans(0); |
评测鸭给出的数据显示,在输入为 $65536(65535)$ 的情况下,采用取模运算的程序运行时间为 $700.94759ms$,而按位与运算的时间仅为 $34.770499ms$。
来说说 HashMap?
我们这里实现拉链 HashMap 的方法是采用拉链法。
拉链法很好理解,对于散射的范围 $[0,M]$,我们建立 $M+1$ 个链表,接下来:
插入
在插入时,我们直接将原 $key$ 散列到 $[0,M]$,然后找到对应的链表将键值对 $key - value$ 插入(注意插入时插入的是未散列的 $key$,因为如果发生了碰撞,就不能用散列值来区分这些碰撞的 $key$ 了 ,查询时需要用原始的 $key$ 来匹配)。
查询
在查询某个 $key$ 时,先把 $key$ 散列到 $[0,M]$,接下来在散列后的值所对应链表中从头到尾寻找是否有与原始的 $key$ 相匹配的键值对 。如果有,则将其 $value$ 作为结果;否则就是查询失败,HashMap 中并没有存储过该键值对。
这里有一张网图作为示意:
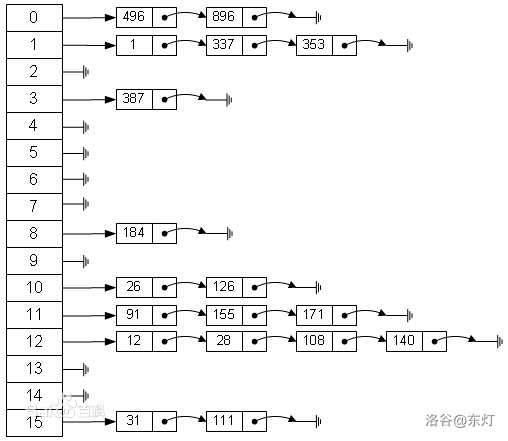
可以发现我们的目的是要开很多很多链表,等于一个链表数组,什么可以快速帮我们解决这个需求呢?
std::forward_list?
C++ 的 STL 中提供了单向链表的实现 std::forward_list,但是常数太大,时间和空间都达不到我们的需求。
手写一个动态开辟空间的链表?
很容易写错,而且操作十分麻烦。
这时候我们想起了图论中的链式前向星,这不正好贴中我们的需求吗!可以将多个链表压到一维,时间和空间的复杂度都很优秀!
开始行动!
首先,我们假定采用的模数为 $P=2^{10}$,而 HashMap 中最多存储 $10^5$ 个键值对。
先定义一个 HashMap 所用的链式前向星节点和 head 数组以及用于统计当前已插入元素的 cnt
1
2
3
4
5
6
unsigned head[1<<10],cnt;
struct edge{
unsigned key,value;//代表一堆 <key-value> 映射
unsigned next;
}e[MAXN];接下来写一个插入函数
1
2
3
4
5inline void insert(unsigned key,unsigned value){
unsigned hashed=key&((1<<10)-1);
e[++cnt]={key,value,head[hashed]};
head[hashed]=cnt;
}再写一个查询函数
1
2
3
4
5inline unsigned find(unsigned key){
for(register unsigned i=key&((1<<10)-1);i;i=e[i].next)
if(e[i].key==key)return e[i].value;
return -1;
}
这样一个很快很快的拉链 HashMap 就完成了。
你这不行,不能弄字符串!
字符串当然可以!
实际上 HashMap 实现存储字符串的方法就是把字符串映射为一个数字的 $key$,然后按照刚才我说的方法处理。
如何映射呢?这里我再推荐一个 $Hash$ 函数(递推形式):$hash(str,i)=hash(str[i-1])*131+str[i]$,最终对于一个字符串的 $hash$ 值即为 $hash(str,str.size())$。
为什么这样处理?因为这样可以保证每一位都有不同的权重,而 $131$ 是字符 $z$ 在 ACSII 表中对应的值的后一个质数,保证了散列的优秀性。
那么我们就可以包装一下,把它变成一个很强大的 HashMap:
1 |
|