圆方树是解决一类仙人掌问题的优秀方法。
广义圆方树是解决无向图路径问题的优秀方法,思路简单暴力且优雅。
这篇文章并不讨论解决仙人掌的圆方树,而是介绍广义圆方树和题目。
Native
定义
圆方树的定义十分简单,就是对于一张无向图(一般讨论的是无向联通图),对于所有点双联通分量,建立一个方点,原图中的边全部删除,一个点双联通分量中的点连接一个方点,这些点就叫做圆点,构成一棵有圆点有方点的“圆方树”。(下图是一张网络上广为传播的圆方树建树流程)
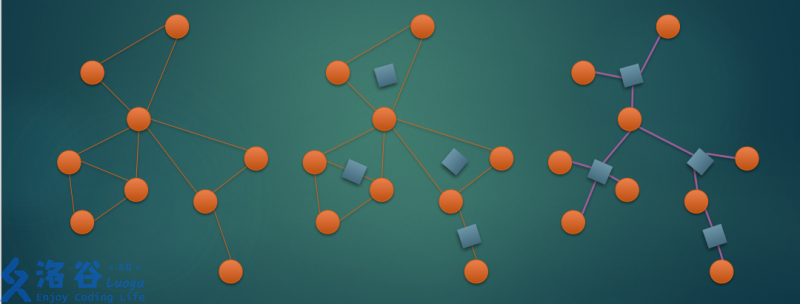
基础性质
那么我们可以通过观察圆方树初步总结出一些毫无用处的性质:
方点不会和方点相连,圆点不会和圆点相连
圆方树是一棵无根树
圆方树貌似非常好建
高级性质
进一步挖掘,可以发现圆方树的优美性质:
- 圆方树可以把原图缩成树,却可以维护原图的连通性
- 割点是圆方树上度大于 $1$ 的圆点
通过高级性质,我们发现:
- 既然圆方树可以维护原图的连通性,我们就可以使用方点维护周围圆点的信息,然后进行树剖等操作来维护两点之间简单路径的信息。
- 既然割点是圆方树上度大于 $1$ 的点,我们就可以轻松的探究图上点与割点本身的关系。
题目
为了不引起题面缩略导致的意义不全,不缩略题面。
CF487E Tourists
圆方树一开始的板子题,可以非常轻松的发现建立圆方树后,可以用方点来维护周围圆点中的最小值,然后树剖寻找最小值即可。
关于带修的问题,修改一个圆点可能修改与之相连的全部方点,菊花图会爆,所以充分利用圆方树的性质,把方点改为维护子树的最小值(建立一个$multiset$),这样每次圆点修改就只需要修改其方点父亲即可。
[POI2008]BLO-Blockade
虽然只是我个人的想法…
我觉得用圆方树做这题的纯属是闲的没事干。
[ZJOI2004]嗅探器
问题可以转化为对于任意一个割点,判断是否可以把 $A$ 点和 $B$ 点断开。
建立圆方树后,如果两个圆点和相同的方点连接,那么就是无解,因为删除哪个点都不能影响它们的通讯。
否则,就可以暴力上跳到它们的 $LCA$,不断寻找度大于 $1$ 的最小编号点。
圆方树有效的忽略了本题中的无用割点(因为他们都不在 $A$ 和 $B$ 所处的子树中),思想又显得比较有趣。