本文在2022年~2023年多次修订，最后一次修订在2023/8/21，如文章有错误请及时反馈。

Tarjan 算法自提出以来，一直作为图论的经典算法被众多 coder 学习。

最近重新摸回 Tarjan，才发现自己对 Tarjan 的实质根本就不理解，仔细学习后作一篇文章来记录。

注意：如果需要阅读学术内容，请直接点击链接下翻到挑战。

批判

在此批判国内部分劣质 blog，其分为两派：

根本不理解就瞎写误人子弟，严谨的算法不是你们认为你们认为就可以的！
所谓详解就是说个定义摆个代码吗？如果把 blog 当做自己的笔记本就请不要说详解！

也许上面的话说的有些过分，下面我就浪费篇幅给大家列举一下以下百度搜索前几项的博客中的错误：

(洛谷P3388题解)题解 P3388 【【模板】割点（割顶）】：一个 SCC 内点的 low 最终不一定一致，该错误我会在下面求 SCC 的时候详细说明。
(CSDN)点双连通分量&边双联通分量详解：对点双定义的修复确实很有价值，但是对于求割点时为什么要判断 root 和 child 的举例图片并非反例，不特判也可以成功找出割点。
(CSDN)割点详解：试问你详解了什么？
(百度知道)图论中的点割集，割点是什么意思：无语。
(搬运后的cnblog)浅谈图的割点和割边（Tarjan）：有向图有割点……？
(洛谷博客)tarjan——割边与割点：“对于 DFS 树根, 判断度数是否大于 1 ”描述错误，root 点可以在图中度数大于1 的情况下在搜索树上的度数仅为 1，搜索树上的 root 大于 1 才可以证明该点为割点。
Tarjan 名字都打错还不是不小心打错的博客不止一个：比如这个，还有这个。

问了好多 OIer，很多的回答也模糊的和这些博客一样，让我怀疑大家都跟喝了假酒一样，着实无奈，故作此文章挑战一下现有互联网博客的说法，以尝试探寻“真正的 Tarjan 算法到底是什么”这一问题的答案。

挑战

阅读之前，希望读者对强连通分量、割点、桥、点双连通分量、边双连通分量的严格定义有一定深度的理解。

一个优美的栈

在正式内容开始前，先介绍一个封装好的栈，很多人的 Tarjan 算法中用了非常隐涩难懂的手写栈，命名还很奇怪（比如 stac,st 之类）这里将其封装起来并声明，下文不再赘述：

struct mystack{
    int values[MAXN],top=0;
    bitset<MAXN>instack;//可维护某元素是否在栈中
    inline void push(int x){
        instack[x]=true;
        values[top++]=x;
    }
    inline int pop(){
        instack[values[--top]]=false;
        return values[top];
    }
}s;

Tarjan-SCC 求有向图的强连通分量(SCC)的算法

在此引入一些概念（From OIWIKI.com）：

有向图的 dfs 生成树主要有 4 种边(不一定全部出现)：

树边(tree edge)：示意图中以黑色边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
反祖边(back edge)：示意图中以红色边表示(即 $7 \rightarrow 1$)，也被叫做回边，即指向祖先结点的边。
横叉边(cross edge)：示意图中以蓝色边表示(即 $9 \rightarrow 7$)，它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点并不是当前结点的祖先。
前向边(forward edge)：示意图中以绿色边表示(即 $3 \rightarrow 6$)，它是在搜索的时候遇到子树中的结点的时候形成的。

对于无向图的 dfs 搜索树上的边的定义类似，只不过不存在横叉边与前向边。

Tarjan 在该算法中提出了两个数组来帮助求得强连通分量，分别为：

dfn：表示到达该点时的 dfs 序。
low：能够回溯到的最早的已经在栈中的结点。设以 $x$ 为根的子树为 $Subtree_x$，$low[x]$ 定义为以下结点的 dfn 的最小值： $Subtree_x$ 中的结点；从 $Subtree_x$ 通过一条不在搜索树上的边能到达的结点。(OIWIKI/李煜东蓝书)

但是在这里我们有一个对于 low 更棒的定义(do-while-true)

因为在图中只有沿着返祖边走 dfn 才可以变小，而横叉边和前向边都是增大，所以上面那句话可以表达为：
low 为 $x$ 最多经过一条返祖边能走到栈中的节点的最小 dfn 为多少。

需要注意的是，Tarjan 算法将会做 dfs 遍历每个点来维护 dfn 和 low，$dfn$ 将会是随时间戳不断严格递增的，而 low 严格非降。

在这里给出的 low 的定义是非常完备的，这点我只在李煜东的蓝书中看到了对此的强调，关于为什么如此定义和栈到底有什么作用在下面的代码中就会说明。

一般的有向图 dfn 和 low 的维护方法如下实现：

inline void tarjan(int x){
    s.push(x);
    dfn[x]=low[x]=++nowtime;
    for(register int i=head[x];i;i=e[i].next){
        int v(e[i].to);
        if(s.instack[v])low[x]=min(low[x],dfn[v]);
        if(!dfn[v]){
            tarjan(v);
            low[x]=min(low[x],low[v]);
        }
    }
    if(dfn[x]==low[x]){
        int k(0);
        do{
            k=s.pop();
        }while(k!=x);
    }
}
int main(){
    for(register int i=1;i<=n;++i)
        if(!dfn[i])tarjan(i);
}

接下来我们来一行一行解析代码：

$line2$：在 $s$ 中将该点压栈，该栈的作用是存放还未被判定为某一 SCC 的点，在发现一个连通块后会弹出到一个位置，弹出的元素构成一个连通块。（具体为什么将在 $line15$ 叙述）
$line3$：dfn[x] 和 low[x] 的初态全部赋值为 ++nowtime(递增的时间)，代表当前结点在不知道接下来的信息时，能到达栈中的 dfn 最小的结点是自己。
$line4-5$：枚举遍历点 $x$ 的出度，并获取出边指向的点。
$line6$：如果该点已经被压栈即该点满足一个性质：该点还未被判定为某一 SCC 中的点。

于是，当前点的 low 向该点的 dfn 询问是否可以经过出点走到更小的点，以更新自己的 low。

在这里引出三个问题（这里的回答需要使用 $line12$ 的描述，可以先行跳读 $line12$）：
- $Q1$：为什么 $line9$ 是 low[x]=min(low[x],low[v])？
- $A1$：这里是 low 定义，刚好是“从 $Subtree_x$ 通过一条不在搜索树上的边能到达的结点。”
- $Q2$：为什么只有栈中的元素才可以更新 $x$ 的 low，而栈外的元素不行
- $A2$：走到栈外的元素的边可能是横叉边也可能是前向边，下面进行分类讨论：
  
  ①如果是横叉边，那么边的出点已经被划归到其他的 SCC 中了，下面用一张图来描述这个问题：可以发现若 1,2,3 已经作为一个 SCC 出栈的情况下，如果 4 指向 3 更新自己的 low 为 1，则4,5,6 这个环路中因为不满足 dfn[x]==low[x] 的条件无论如何也不能判断自己是一个环了。
  
  ②如果是前向边，那么 dfn[v]>low[x]，一定不会发生更新，也没必要再去更新了。
- $Q3$：为什么有些代码中 $line6$ 写 low[x]=min(low[x],low[v]) 依旧正确？
- $A3$：可以发现这种写法实际上是不符合该算法思想的，因为 low 的定义是只能经过一条不在搜索树上的边，而 low[v] 的意义是可能经过多条不在搜索树上的边，其正确性只在 Tarjan-SCC 算法和 Tarjan-Bridge 算法中才保有。这种方法可以侥幸正确的原因是：对于有向图来说，走到一个在栈中而且已经走过的点，那么其一定是一条返祖边或者前向边，我们进行分类讨论：
  
  ①如果是前向边，那么使用 low 或者 dfn 来更新都是一样的，因为无论如何都满足 dfn[v],low[v]>low[x]，不会发生更新。
  
  ②如果是返祖边，那么使用 low 和 dfn 都会发生更新，而一个点可能有多条返祖边，构成多个环，这些环之间具有一定的交集，考虑该点处在最大环上和最大环内的情况，如果处在最大环上，那么无论如何返祖，最终其 low 都将变成该 SCC 的根的 dfn。而如果是在最大环内的点，如果指向的是栈内的点，那么可以保证的是被指向点(设为 $v$)与的指出点(设为 $u$)一定满足 dfn[u]>low[v]，则点 $u$ 就会满足 dfn[u]>low[u]，在回溯到 1 之前不会发生出栈，因此是正确的。
  
  从这个问题可以发现求 SCC 中正确性保证的条件：只要让除了 SCC 的根之外的所有点 dfn!=low，那么实际上算法就是正确的。
$line7-10$：若 dfn[v]=0，则在此进一步深搜，即该点没有走过，继续进行下一步深搜。同时，在回溯时更新该结点的 low 值，因为这里是沿树边的深搜，因此可以直接用 low[x]=min(low[x],low[v]) 来更新该结点的 low 的值。证明很显然：因为树边路径上的点的 low 最终是经过一条返祖边指向该点所在的最大环上 dfn 最小的祖先，满足 low 数组只经过一条返祖边的定义。
$line12-17$ 对于一个 SCC 内某个最大环的 dfn 最小即深度最小的祖先 $x$，在 dfs 回溯时若 dfn[x]==low[x]，则可说明该点不能通过返祖边到达 dfn 更小的祖先，自己或者和自己 dfs 子树中的部分点构成一个 SCC。接下来从栈中出栈，直到出栈到遇到 $x$ 元素，这些元素就构成一个 SCC。

证明：首先考虑栈顶元素的性质，一定存在一条有向路径从 $x$ 通往栈顶元素。对于栈中 $x$ 之后入栈的元素且回溯到 $x$ 时还在栈中的元素，一定满足 $low \not =dfn$，因为若 $low=dfn$，将先一步出栈，若 $low\not=dfn$，则栈顶元素一定通过一条返祖边走向一个搜索树上的祖先，而且该点不可能指向 $x$ 的祖先，否则 $low[x]<dfn[x]$，若指向的是 $x$ 或 $x$ 的子树上的祖先，则分类讨论：

①第一种情况为被指向的点到栈顶元素之间的点与 $x$ 之间没有返祖边，这种情况下被指向的点将会先满足 $dfn[x]=low[x]$ 的条件先一步连带栈顶出栈，不可能与 $x$ 处在同一栈中。

②第二种情况为被指向的点到栈顶元素之间的点与 $x$ 之间x有返祖边，则这种情况下存在一个环经过 $x$ 到栈顶元素又到栈顶元素返祖边指向的点再到具有回到 $x$ 的返祖边的点再回到 $x$ 的环，构成一个 SCC。

③第三种情况为被指向的点就是 $x$，此时 $x$ 到栈顶元素的路径构成一个环，为一个 SCC。

这里采用了一种类似递归的论证方式，先假设当前已经到了某一步，之前步遇到 $dfn[x]=low[x]$ 时将元素出栈的处理是正确的，进一步证明了当前步的处理的正确的，即可递归式的将该结论推广到全局证明这个结论的正确性。

细心的读者也许发现了，这种论证方式可以合理的后推，而不能说明第一次这样做的时候可以求得 SCC，对于此的论证，可以仿照上述的论证模式，首先栈顶元素不可能指向 $x$ 的祖先，接下来再抓住条件 $dfn[x]=low[x]$ 是第一次被满足，如果是上述①中的情况，子树中有点满足 $dfn=low$ 的点，那么$x$一定不是第一个满足条件的点，所以只能采用上述②中的情况，构成一个 SCC。

按照以上论证的思路可以发现经过 Tarjan-SCC 算法求出的强连通分量按编号形成逆拓扑序，这是一个十分重要的性质。

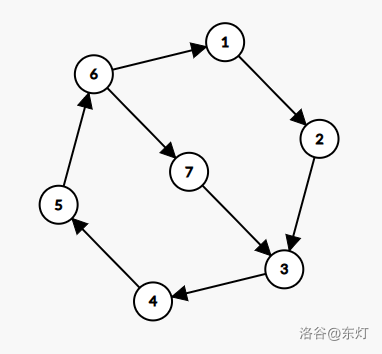
更严谨的证明还需要说明环内部的路径并不影响结果，这是一个自然语言难以叙述但是非常显然正确的结论：如果有一条路径从环上一点能够到达环上的另外一点，那么实际上就构成了一个更小的环，与最大环的点之间均可互相到达，因此实际上无需担心小环包含在大环中的情况如何处理。比如下图，大环为($1\rightarrow2\rightarrow3\rightarrow4\rightarrow5\rightarrow6$)，小环为($6\rightarrow7\rightarrow3\rightarrow4\rightarrow5$)

实际上，该图可以作为洛谷割点某个题解中一个说法的反例：求解 SCC 时候，SCC 内所有点的终态是 $dfn=low$。

此处中的证明思路能证明该算法的正确性，与 Tarjan 的《$\mathcal{Depth-first \ search \ and \ linear \ graph \ algorithms}$》中思路并不相同，如果上述证明还有部分不严谨不清楚的地方1，也希望大家可以向我指出。
$line20-21$：枚举图中每个点，当遇到 dfn==0 的点即还未被搜索过的点便开始搜索，最终可以保证全部点都被搜索。

若如果求出了 SCC，因为一个 SCC 内的点均可互相到达，在处理某些问题的时候就可以进行缩点处理，但是不属于本文探讨的问题范畴，故在此处不详细展开了。

Tarjan-CutPoint 求无向图割点的算法

延续刚才的话题，下面给出无向图中维护 $dfn$ 与 $low$ 的代码实例：

void tarjan(int x){
	dfn[x]=low[x]=++nowtime;
	for(register int i=head[x];i;i=e[i].next){
		int v(e[i].to);
		if(!dfn[v]){
			tarjan(v);
			low[x]=min(low[x],low[v]);
		}else low[x]=min(low[x],dfn[v]);
	}
}

可以发现这里 low 数组的意义变为了最多经过一条返祖边能走到的 dfn 最小的结点为多少，为什么少了一个“在栈中”呢？

在求 SCC 的时候，我们发现判断是否在栈中是为了避免横叉边和前向边对结果产生影响，但是可以发现的是，无向图中并没有这两种性质的边，所以没有必要进行特殊的处理。

正是因为上面的原因，李煜东的蓝书中选择将无向图连通性一节放在有向图连通性一节之前，能够看出这是一个经过慎重考虑和斟酌的决定。

下面来看如何求割点，先考虑割点在 dfs 搜索树上的性质，容易发现第一个割点判定法则：
若回溯时 dfn[x]<=low[v] 且 $x$ 并非搜索树的根，则 $x$ 为割点。

为什么如此呢？考虑 $x$ 不是树根时，当 dfn[x]<=low[x]，这意味着自己以及自己子树中的结点无论怎么走最早到达的最小结点是自己或者自己靠后的结点，如果要到达 $dfn$ 更小的结点即 $x$ 的祖先，只能通过 $x$ 点到达，若删去 $x$，则图不连通，割点成立。

这个判据对 $x$ 是搜索树根时无效，因为树根没有父亲，dfn 就是最小的，如果采用上述条件来判断，子树无论如何也不能用返祖边返回 dfn 更小的结点以逃避 $x$ 是个割点，然而事实真的如此吗？看一张图：

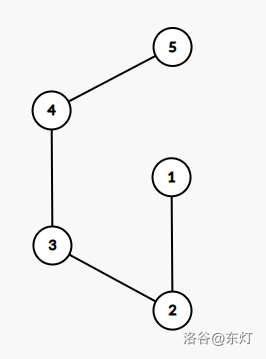
该图是一个链，如果 1 是根结点，将会被判断为割点，而实则 1 并非割点。因此对于根结点，不能通过子结点无法到达根结点的任何祖先来判断根结点是否是割点，因为其根本就没有祖先，自然也不能说子结点只能通过该点到达其他点了。

对于根结点是割点的情况，只有根结点具有两个及以上子树时，因为无向图的搜索子树之间互相独立(没有横叉边、前向边导致的必然情况)，所以没有根结点是不能互相到达的，此时根结点就是一个割点。因此得出割点的第二判定法则：

若回溯时 $x$ 为搜索树的根且其在搜索树上有两个及以上的子树时候，则 $x$ 为割点。

接下来就可以给出割点的代码实现：

void tarjan(int x){
	dfn[x]=low[x]=++nowtime;
	int child(0);
	for(register int i=head[x];i;i=e[i].next){
		int v(e[i].to);
		if(!dfn[v]){
			tarjan(v);
			++child;
			low[x]=min(low[x],low[v]);
			if(x==root&&child>1)cutpoint[x]=true;
			else if(x!=root&&dfn[x]<=low[v])cutpoint[x]=true;
		}else low[x]=min(low[x],dfn[v]);
	}
}
int main(){
	for(register int i=1;i<=n;++i)
		if(!dfn[i]){
			root=i;
			tarjan(i);
		}
}

特别需要注意的是，割点可能被重复标记，当且仅当该割点不为根结点且具有多棵子树时，因此上述代码使用了一个布尔数组来对割点进行标记。

Tarjan-Bridge 求无向图桥的算法

在 Tarjan 求解无向图的桥时，一大争议是 low 的定义是否发生了变化，在此鄙人的理解是，low 的定义应发生变化。

与其每次都说 low 的定义不变，只是求解不同的东西时做了特判，不如说在求解每种东西的时候因为需求不同，low 的定义也随之变化。

在求桥时，low 的新定义应为最多经过一条非指向父亲的返祖边能走到的 dfn 最小的结点为多少。

为什么这里又变成了不能指向父亲呢？这事实上与桥的判断法则有关，我们尝试仿照割点判断法则的推导方式来推导：

若回溯到 $u$ 点时时存在一条树边 $(u,v)$，满足 dfn[u]<=low[v]，则分别考虑等于与不等于的情况：

①考虑若 dfn[u]<low[v]，那么证明 $v$ 一定不能通过某条路回到 $u$，$(u,v)$ 为桥。

②考虑若 dfn[u]>=low[v]，那么有可能是 $v$ 通过自己子树上的点的返祖边到达了 $u$ 或 $u$ 的祖先，$(u,v)$ 不为桥。但是如果不忽略指向父亲的返祖边，会导致每一条树边的 $(u,v)$ 都满足 dfn[u]>=low[v]。因为对于 $v$ 来说，$(v,u)$ 是一条返祖边，low[v] 会被更新为 dfn[u]，接下来更新只会越来越小，因此即使 $(u,v)$ 是桥，在不忽略指向父亲的返祖边的情况下，也会被判定为非桥，这就是在求桥时 low 的定义要发生改变的原因。

接下来我们看一下求桥的代码：

void tarjan(int x,int father){
	dfn[x]=low[x]=++nowtime;
	for(register int i=head[x];i;i=e[i].next){
		int v(e[i].to);
		if(!dfn[v]){
			tarjan(v,i);
			low[x]=min(low[x],low[v]);
			if(low[v]>dfn[x])bridges[i]=bridges[i^1]=true;
		}else if(i!=(father^1))low[x]=min(low[x],dfn[v]);
	}
}
int main(){
	for(register int i=1;i<=n;++i)
		if(!dfn[i])tarjan(i,0);
}

对于这里的代码有必要做出一些解释：

$line1$：father 为祖先走向 $x$ 的所走的路径，在 $line6$ 中 $i$ 为走到 $x$ 的来向边，因此传到下一步深搜作为 father。
$line8-9$：这里采用了对边的编号异或 1 的操作，在于利用无向图存边是下标相邻的两条边的性质，某个自然数 $xor \ 1$ 满足“小偶变大奇，大奇变小偶”的性质，如果边从 2 开始存，那么已知一条边的编号，就可以求出对应的反向边。对于 $line9$ 中条件 $i\not=(father\ xor \ 1)$，而这里判断的就是当前边 $i$ 是否为来时边的反向边即返回父亲的边。

有一个问题：
- $Q$：为什么 $line9$ 位置填 low[x]=min(low[x],low[v]) 又对了，难道只有判断割点需要写 low[x]=min(low[x],dfn[v]) 吗？
- $A$：说实话，你说的对，除了割点有关的算法之外，low[x]=min(low[x],low[v]) 都是正确的，但是从对于算法原始理解的角度出发，这种正确是侥幸的，对于 SCC 为什一个么的正确的已经在上面论证过了，接下来我们论证为什么这种更新方式在桥中是正确的：
  
  可以注意到无向图中没有前向边，只有树边和返祖边，而发生 $line9$ 更新的只能是返祖边。所以说，要论证这种更新方式在判断桥时是正确的，只需论证出现返祖边时采用这种更新方式在判断桥时不会产生错误。
  
  那么考虑有一返祖边 $(x,y)$，则 $x$ 到被指向的点 $y$，$y$ 到 $x$ 的在搜索树上的路径将形成一个环路，又因为一定存在 low[y]<= dfn[y]，所以可以肯定的是在搜索树上的这个环路在最终回溯时都会被更新为被指向点的 low。
  
  显然可知环上不会出现桥，那么根据上面的推论，这保证了环上不会出现桥，再把该环视为一个整体，考虑环与外面的连边，我们假设一边为 $(u,v)$，那么所用到的是 dfn[u] 与 low[v]，可以发现 $u$ 点虽然在环上，但是 dfn[u] 只与搜索的顺序有关，而 low[v] 如何更新与这个环无关。
  
  我们可以来试一试：如果 $(u,v)$ 是返祖边，那么有可能返回环上的点，也可能返回的是环的祖先，易发现的是一定存在 dfn[u]>=low[v]，其一定不为桥，这是正确的。如果 $(u,v)$ 是树边，那么如果 $v$ 和 $v$ 的子树都不能返祖，就不会发生 $line9$ 的更新，只能假设 $v$ 或 $v$ 的子树上的点会返祖，那么假设 $v$ 或 $v$ 的子树中的点返回环上的点和返回环的祖先的情况都已经讨论过了，但是有可能出现 $v$ 的子树中的点返回 $v$ 的子树内点的情况，又构成一个小环，但是我们在这一步只需考虑该环是否对 $(u,v)$ 是否为桥的判断造成影响，显然答案是否定的。
  
  这个论证方法实际与求 SCC 中提到的递归论证方法是不同的，因为其没有先假设这种更新方式是正确的，而是直接套用该更新方式进行更新并分类讨论更新中可能会遇到的各种情况来论证判断桥时的错误是不可能发生的，因此其对每个环的证明之间都是相互独立的。再考虑我们的证明目的是只需要对所有环证明该更新方式在判断桥时正确，所以直接对搜索树中的所有环套用该证明即可。
  
  很多读者就会产生疑惑：那为什么割点不行呢？
  
  可以注意到的是除了对于根结点的特别处理之外，割点和桥的判断条件不同仅在 dfn[u]<=low[v] 中的一个等号，这个等号实际上是至关重要的。
  
  考虑一种情况，有一条返祖边 $(u,v)$，此时假设 $v$ 通过返祖边到达过祖先，那么low[v]<dfn[v]，根据 low[u]=min(low[u],low[v]) 的更新规则，$v$ 到 $u$ 的树边路径上的 low 都会被更新为 low[v]，而又因为 low[v]<dfn[v]，因此即使此时 $v$ 是一个割点，也无法被判断出来。下图的搜索树( 1 为根结点)表明了这种错误发生的场景：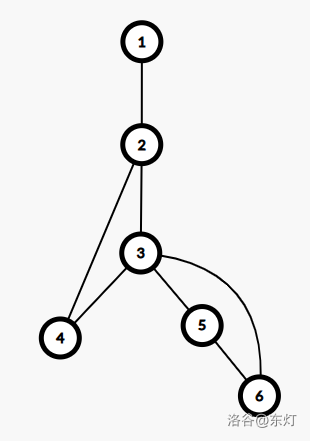
  
  该图中，点 3 为割点，但是如果采取 low[x]=min(low[x],low[v]) 的更新方式其并不会被判断为割点。究其原因，是因为对于判断割点时在条件 dfn[u]<=low[v] 中需要取等号才能判断成功的割点$^{[1]}$可能有不能判断其为割点的子树或自身返祖到更小的结点导致出现 $low<dfn$ 的情况，导致在另外一棵能判断其为割点的子树中的点返祖到该点时候 low 上翻到该割点的祖先发生错误。
  
  注：
  
  [1] 忽略每次搜索根结点之外，这种割点实际上和 SCC 的根类似(不过判断 SCC 的时候成立条件也是 dfn==low，很难说他俩没啥联系)，就是每个搜索树上的环在搜索树上 $dfn$ 最小的结点，这种结点具有“被返祖”的性质，也就是说子树中一定有指向这个“根”点自身的返祖边。而如果这种“根”点是割点，那么还需要保证这个环路中的所有点是相对“封闭的”，最早也就只能回溯到这个“根”点。上文中“能判断其为割点的子树”实际上就是指的能够构成这种相对“封闭”的环的子树。
$line 14$：因为搜索树的根结点不存在父亲，因此 $father$ 传入什么都是不影响判断的，因为对于根结点一定不会发生 $line9$ 的更新。

Tarjan-V-DCC 求无向图点双连通分量(V-DCC)的算法

接下来我们将开始讨论双连通分量的问题，首先是点双连通分量。

在文章的开始位置已经提醒过读者需要对各种连通分量的概念有一定的了解，因为关于双连通分量定义的完善和补充并不是本篇文章的讨论内容。

对于点双连通分量的求法，我们仅需考虑：每个割点将处于两个点双连通分量中，感性理解一下就是两个割点之间夹了一个点双连通分量。

以上明确后，接下来我们看代码：

inline void tarjan(int x){
    dfn[x]=low[x]=++nowtime;
    s.push(x);
    if(x==root&&head[x]==0){
        dcc[++dcccnt].push_back(x);
        return;
    }
    for(register int i=head[x];i;i=e[i].next){
        int v(e[i].to);
        if(!dfn[v]){
            tarjan(v);
            low[x]=min(low[x],low[v]);
            if(low[v]>=dfn[x]){
                ++dcccnt;
                int k;
                do{
                    k=s.pop();
                    dcc[dcccnt].push_back(k);
                }while(k!=v);
                dcc[dcccnt].push_back(x);
            }
        }else low[x]=min(low[x],dfn[v]);
    }
}
int main(){
    for(register int i=1;i<=n;++i)
        if(!dfn[i]){
            root=i;
            tarjan(i);
        }
}

代码中有一部分需要特别强调的点：

$line4-7$：这是对孤立点的处理，因为孤立点在定义中也算作一个点双连通分量。
$line13-21$：这里搜索到了一个割点，把到上个割点为该割点的所有点全部出栈压入同一个点双连通分量中。

这里有一个问题：
- $Q$：这里的割点判定为什么只考虑了 dfn[x]<=low[v] 的判断条件而没有考虑 $x$节点为 root 时的情况？
- $A$：可以，但是没必要。
  
  考虑 x=root 时 $x$ 为割点的条件 son>1，在这种情况下 root 和另外一个节点为一个点双连通分量的两端，这种情况下 $x$ 点无论是否视为割点，都会被划入该点双连通分量内，因此说“可以，但是没必要”。

Tarjan-E-DCC 求无向图边双连通分量(E-DCC)的算法

求解无向图的边双连通分量有两种方法，有一种很好理解的办法是：由于边双连通分量中不存在桥，所以实质上只需要把桥全部求出来再跑一遍不过桥的 dfs 即可求出边双连通分量。

void tarjan(int x,int father){
	dfn[x]=low[x]=++nowtime;
	for(register int i=head[x];i;i=e[i].next){
		int v(e[i].to);
		if(!dfn[v]){
			tarjan(v,i);
			low[x]=min(low[x],low[v]);
			if(low[v]>dfn[x])bridges[i]=bridges[i^1]=true;
		}else if(i!=(father^1))low[x]=min(low[x],dfn[v]);
	}
}
void dfs(int x){
    vis[x]=1;
    for(register int i=head[x];i;i=e[i].next){
        if(bridges[i])continue;
        int v(e[i].to);
        if(!vis[v])dfs(v);
    }
}
int main(){
	for(register int i=1;i<=n;++i)
		if(!dfn[i])tarjan(i,i);
    for(register int i=1;i<=n;++i)
        if(!vis[i]){
            dfs(i);
            ++dcccnt;
        }
}

第二种求解方法可以联系求解 SCC 时的知识理解：在求桥时限制了返回父亲的返祖边的情况下，在选定 root 节点之后，一张无向图已经变成了一张有向图（实际上这张有向图就是搜索树），往什么方向走，什么地方会在搜索树上形成有向环，都已经是固定下来的了。因此我们可以仿照求 SCC 时的思路，在一个强连通分量中的点可以互相到达，而处于两个不同强连通分量中的点不能相互到达，而边双连通分量恰好是没有桥的连通分量，我们引出一个非常容易想的结论：在无向图中只要一个分量中没有桥，那么该分量在 Tarjan-Bridge 算法抽象出的有向图中一定强连通，反过来说，被抽象为有向图的无向图中的一个强连通分量，在原图中是一定一个边双连通分量。因此在已经被抽象成有向图的无向图中，我们只需求出强连通分量就恰恰是边双连通分量。

对上述结论作一个简要但不严谨的说明：考虑 Tarjan-Bridge 算法实际上抽象出的有向图实际上就是一棵搜索树，而在该搜索树上构成环当且仅当出现返祖边，即在无向图中该分量内不会出现桥，容易发现的是搜索树最终可以被划分为类似环-桥-环的结构，与边双连通分量的定义实际上是相符的。关于其为什么是极大的，这点可以参照前文中对于求 SCC 算法中解释“为什么环内路径不影响结果”的部分。

这样想的话，实际上这种方法是把无向图抽象为有向搜索树，通过搜索树的性质利用对于有向图求 SCC 的方法求出边双连通分量，这种抽象方式令人拍手称妙。

代码如下：

void tarjan(int x,int father){
	dfn[x]=low[x]=++nowtime;
	s.push(x);
	for(register int i=head[x];i;i=e[i].next){
		int v(e[i].to);
		if(!dfn[v]){
			tarjan(v,i);
			low[x]=min(low[x],low[v]);
		}else if(i!=(father^1))low[x]=min(low[x],dfn[v]);
	}
	if(dfn[x]==low[x]){
		++dcccnt;
		int k;
		do{
			k=s.pop();
			belong[k]=dcccnt;
		}while(k!=x);
	}
}
int main(){
	for(register int i=1;i<=n;++i)
		if(!dfn[i])tarjan(i,i);
}

东灯的寒舍

批判与挑战——真正的Tarjan算法到底是什么

批判

挑战

分类